An open circular vessel is 1m in diameter and 2m height. It contains water filled to a depth of 1.5m. If the cylinder rotates about its vertical axis, (a) what constant angular velocity can be obtained without spilling, (b) what is the pressure intensity at the center and at the corner of the bottom if ω = 6 radians/seconds.

Problem Statement

An open circular vessel is 1 m in diameter and 2 m in height. It contains water filled to a depth of 1.5 m.

If the cylinder rotates about its vertical axis:

1. (a) What constant angular velocity can be obtained without spilling?
2. (b) What is the pressure intensity at the center and at the corner of the bottom if \( \omega = 6\,\text{rad/s} \)?

Solution

1. Given:

   Diameter = 1 m  ⇒ \( r = 0.5\,\text{m} \)
   Vessel Height = 2 m  Initial water depth = 1.5 m
   \( g = 9.81\,\text{m/s}^2 \)  \( \gamma = 9810\,\text{N/m}^3 \)

2. Part (a): Maximum Angular Velocity without Spillage

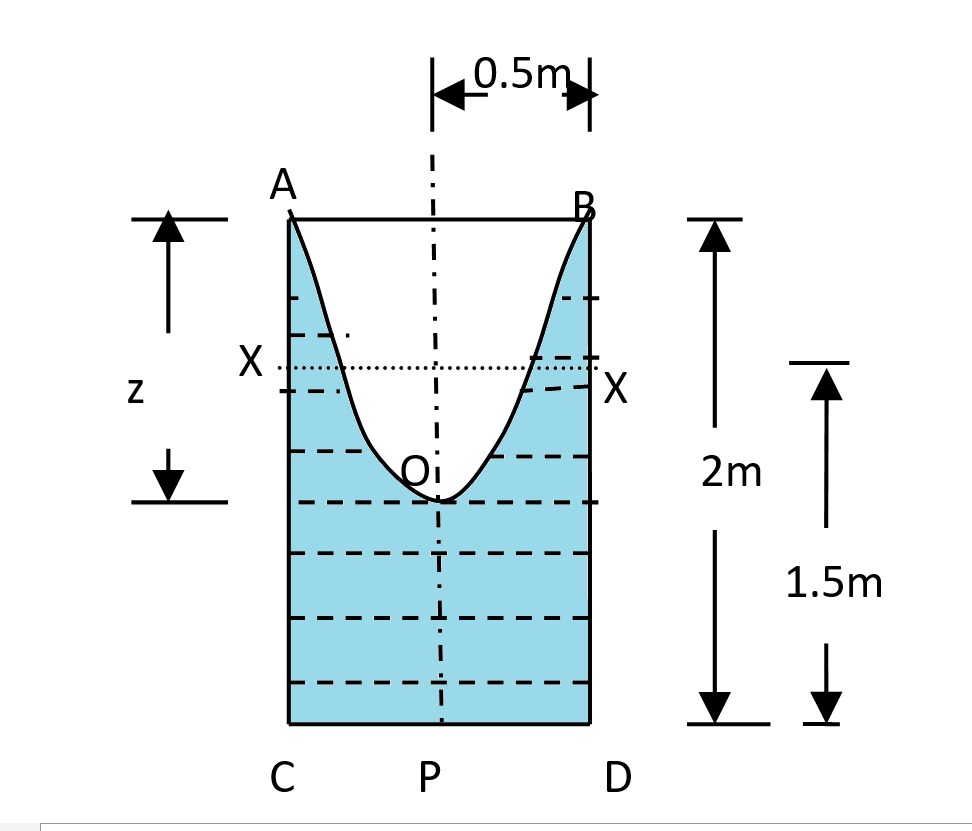
   With 1.5 m of water in a 2 m tall vessel, there is a 0.5 m clearance from the undisturbed free surface (denoted \( XX \)) to the top rim. Under rotation the free surface forms a parabola. At maximum rotation the rise at the edge above \( XX \) equals the fall at the center below \( XX \); that is,

   \( \frac{z}{2} = 0.5\,\text{m} \quad\Longrightarrow\quad z = 1\,\text{m} \)

   The free surface depression is related to the angular velocity by:

   \( z = \frac{r^2\,\omega^2}{2g} \)

   Substituting \( r = 0.5\,\text{m} \) and \( z = 1\,\text{m} \):

   \( 1 = \frac{(0.5)^2\,\omega^2}{2 \times 9.81} \)

   Solving for \( \omega \):

   \( \omega^2 = \frac{2 \times 9.81}{0.25} \approx 78.48 \quad\Longrightarrow\quad \omega \approx 8.858\,\text{rad/s} \)

   Converting to revolutions per minute:

   \( N = \frac{60\,\omega}{2\pi} \approx 85\,\text{rpm} \)

3. Part (b): Pressure Intensity for \( \omega = 6\,\text{rad/s} \)

   For \( \omega = 6\,\text{rad/s} \), the free surface depression is:

   \( z = \frac{(0.5)^2 \times 6^2}{2 \times 9.81} \approx 0.46\,\text{m} \)

   The vertex of the parabola (point \( O \)) is \( \frac{z}{2} \) below \( XX \):

   \( \frac{0.46}{2} \approx 0.23\,\text{m} \)

   Therefore, the effective water depths become:

   \( h_1 = 1.5 – 0.23 = 1.27\,\text{m} \) (at the center)
   
   \( h_2 = 1.5 + 0.23 = 1.73\,\text{m} \) (at the corner)

   The corresponding pressures are:

   \( P_{\text{center}} = \gamma\,h_1 = 9810 \times 1.27 \approx 12459\,\text{Pa} \)
   
   \( P_{\text{corner}} = \gamma\,h_2 = 9810 \times 1.73 \approx 16971\,\text{Pa} \)

Explanation

When the vessel rotates, centrifugal forces cause the water’s free surface to assume a parabolic shape. In part (a), the maximum angular velocity is determined by ensuring that the raised edge of the water just touches the top rim. In part (b), a lower rotation rate (\( \omega = 6\,\text{rad/s} \)) results in a less pronounced free surface deformation; the vertex of the parabola is 0.23 m below the undisturbed level, leading to different effective water depths at the center and the edge.

Physical Meaning

This problem demonstrates the impact of rotation on the free surface and pressure distribution in a partially filled vessel. The analysis shows how the maximum allowable angular velocity is limited by the available clearance to prevent spillage, and how rotation alters the hydrostatic pressure at the bottom—critical considerations in the design and operation of rotating fluid systems.