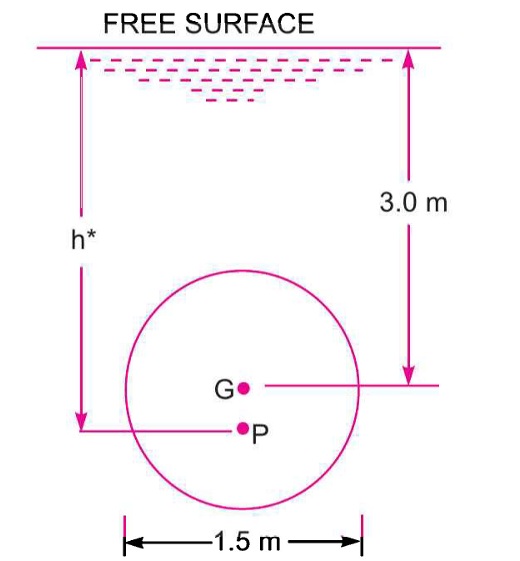
A float valve regulates the flow of oil (sp. gr. 0.8) into a cistern. The spherical float is 15 cm in diameter. A weightless link AOB carries the float at B and a valve at A. The link is hinged at O, with ∠AOB = 135°. OA = 20 cm and OB = 50 cm. When flow is stopped, AO is vertical and the oil surface is 35 cm below the hinge. A force of 9.81 N is required on the valve to stop the flow. Determine the weight of the float.
Float Valve Equilibrium Problem Problem Statement A float valve regulates the flow of oil (sp. gr. 0.8) into a cistern. […]