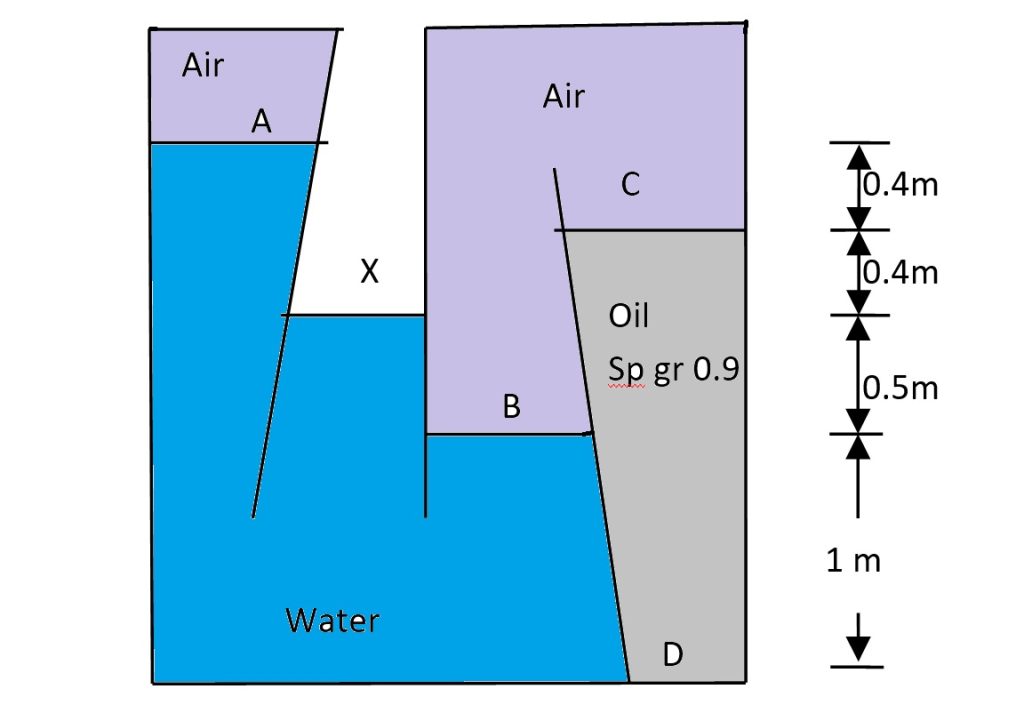
Problem Statement
Calculate the pressures at points A, B, C, and D in the figure. Assume the tube is filled with oil of specific gravity \( 0.9 \).
Solution
Given:
- Specific weight of water (\( \gamma \)) = \( 9810 \, \text{N/m}^3 \)
- Specific gravity of oil = \( 0.9 \)
- Specific weight of oil (\( \gamma_{\text{oil}} \)) = \( 0.9 \times 9810 = 8829 \, \text{N/m}^3 \)
- Take atmospheric pressure as 0 for gauge pressure.
Pressure at A (\( P_A \)):
Using the hydrostatic pressure equation:
\( P_A = 0 – \gamma h_{\text{between X and A}} \)
Substitute the values:
\( P_A = – (9810 \times 0.8) \)
Final Value:
\( P_A = -7848 \, \text{Pa} \)
Pressure at B (\( P_B \)):
Using the hydrostatic pressure equation:
\( P_B = 0 + \gamma h_{\text{between X and B}} \)
Substitute the values:
\( P_B = 9810 \times 0.5 \)
Final Value:
\( P_B = 4905 \, \text{Pa} \)
Neglecting air, the pressure at C (\( P_C \)) is:
\( P_C = P_B = 4905 \, \text{Pa} \)
Pressure at D (\( P_D \)):
Using the hydrostatic pressure equation:
\( P_D = P_C + \gamma_{\text{oil}} h_{\text{between C and D}} \)
Substitute the values:
\( P_D = 4905 + (8829 \times 1.9) \)
Final Value:
\( P_D = 21680 \, \text{Pa} \)
Explanation
This problem involves calculating the pressures at different points within a fluid-filled tube using hydrostatic principles:
- The pressure at A (\( P_A \)) is calculated as negative due to the height of water above it, relative to atmospheric pressure.
- The pressure at B (\( P_B \)) is determined by the height of the water column from point X to B.
- Since air pressure is neglected, the pressure at C (\( P_C \)) is equal to \( P_B \).
- The pressure at D (\( P_D \)) is calculated by adding the pressure contribution from the oil column between points C and D to \( P_C \).
Physical Meaning
- Specific Weight: The specific weight of a fluid determines the pressure it exerts for a given height. Here, oil’s specific weight is less than water’s, leading to different pressure contributions.
- Gauge Pressure: All calculations assume atmospheric pressure as the reference (0 gauge pressure), simplifying the analysis.
- Layered Fluids: The pressure at different points depends on the height and specific weight of the fluids present in the column.
