The diameters of the limbs A and B of a U-tube shown in fig. are 5mm and 20mm respectively. The limb A contains a liquid of sp. gr. 0.9 while the limb B contains a liquid of sp.gr. 1.3.

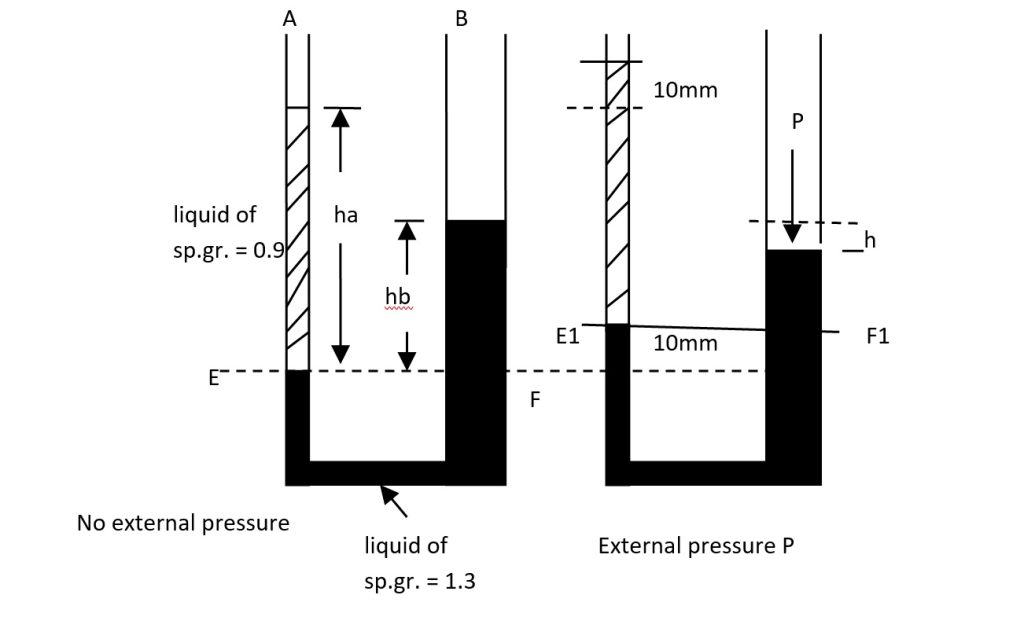
Problem Statement

The diameters of the limbs A and B of a U-tube are 5 mm and 20 mm, respectively. The limb A contains a liquid with a specific gravity of 0.9, while the limb B contains a liquid with a specific gravity of 1.3. If an external pressure is applied on the surface of the liquid in limb B to cause a 10 mm rise in the liquid level in limb A, determine the required pressure.

Given data:

Specific gravity of liquid in A (γ_A) = 0.9
Specific gravity of liquid in B (γ_B) = 1.3
Diameter of limb A = 5 mm
Diameter of limb B = 20 mm

Solution

1. Initial Pressure Balance

Without external pressure, the equilibrium equation is:

\(γ_A \times h_A = γ_B \times h_B\)

\(0.9 \times 9810 \times h_A = 1.3 \times 9810 \times h_B\)

\(h_A = \frac{1.3 \times h_B}{0.9} \tag{1}\)

2. Effect of External Pressure

When external pressure is applied to limb B, the rise in level in limb A is 10 mm, and the fall in limb B is \(h\). Using volume conservation:

\( \text{Cross-sectional area of limb A} \times 10 \times 10^{-3} = \text{Cross-sectional area of limb B} \times h \)

\( \frac{\pi}{4} \times (5 \times 10^{-3})^2 \times 10 \times 10^{-3} = \frac{\pi}{4} \times (20 \times 10^{-3})^2 \times h \)

\(h = 0.000625 \text{ m} \tag{2}\)

3. Pressure Balance with External Pressure

At the new equilibrium, the pressure equation becomes:

\( γ_A \times \left(h_A + 10 \times 10^{-3}\right) = P + γ_B \times \left(h_B – 10 \times 10^{-3} – h\right) \)

Substituting values:

\(0.9 \times 9810 \times h_A = P + 1.3 \times 9810 \times (h_B – 0.010625) \tag{3} \)

Combining equations (1), (2), and (3):

\(8829 \times \frac{1.3 \times h_B}{0.9} = P + 12753 \times (h_B – 0.010625) \)

Solving for \(P\):

\(P = 135.5 \text{ N/m}^2\)

Required external pressure:

\(P = 135.5 \text{ N/m}^2\)

Explanation

Initial Pressure Balance: The liquids in the U-tube initially balance based on their specific weights and heights.
Volume Conservation: The rise in one limb equals the fall in the other limb, adjusted for their cross-sectional areas.
External Pressure: The applied pressure modifies the equilibrium, resulting in a measurable rise in limb A and fall in limb B.
Final Calculation: By combining the principles of hydrostatics and volume conservation, the required external pressure is determined.

Physical Meaning

This problem illustrates the interplay between pressure, specific weights, and volume conservation in a U-tube. Such calculations are crucial in understanding fluid dynamics in interconnected systems and designing pressure-based measurement devices like manometers.