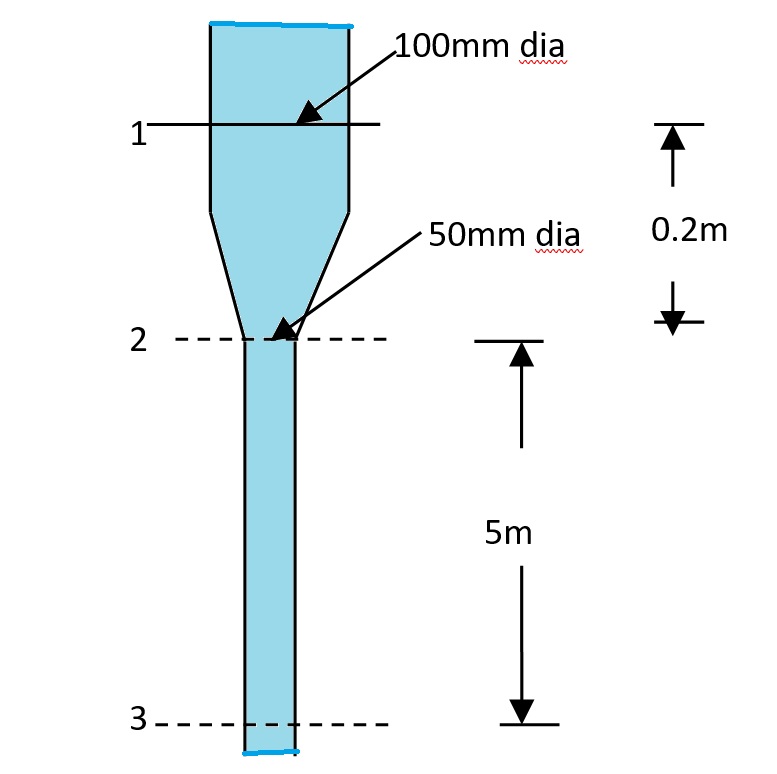
Determination of Jet Diameter 5m Below the Nozzle
Problem Statement
A jet of water is coming out from a 50mm diameter rounded nozzle attached to a 100mm diameter pipe and is directed vertically downwards. If the pressure in the 100mm diameter pipe 0.2m above the nozzle is 200 kPa gauge, determine the diameter of the jet 5m below the nozzle level.
Given Data
| Pipe Diameter at Section 1 (d₁) | 100 mm = 0.1 m |
| Nozzle Diameter at Section 2 (d₂) | 50 mm = 0.05 m |
| Pressure at Section 1 (P₁) | 200 kPa gauge |
| Elevation Difference (Z₁ – Z₂) | 0.2 m (above nozzle) and 5 m drop below nozzle) |
| Acceleration due to Gravity (g) | 9.81 m/s² |
1. Areas and Velocities at Sections 1 & 2
Section 1 (Pipe):
Diameter, d₁ = 0.1 m
Cross-sectional Area, A₁ = (π/4) × d₁² = (π/4) × (0.1)² = 0.007854 m²
Section 2 (Nozzle):
Diameter, d₂ = 0.05 m
Cross-sectional Area, A₂ = (π/4) × d₂² = (π/4) × (0.05)² = 0.001963 m²
Continuity Equation:
A₁V₁ = A₂V₂ → V₁ = (A₂/A₁) V₂ = 0.25 V₂
2. Applying Bernoulli’s Equation (Sections 1 to 2)
Taking datum at the nozzle (Section 2):
P₁/γ + (V₁²)/(2g) + Z₁ = P₂/γ + (V₂²)/(2g) + Z₂
Given: P₁ = 200 kPa = 200,000 N/m², P₂ = 0 (atmospheric), Z₁ = 0.2 m, Z₂ = 0 m
Substitute:
(200,000 / 9810) + (V₁²)/(2×9.81) + 0.2 = 0 + (V₂²)/(2×9.81)
Calculate Pressure Head: 200,000/9810 ≈ 20.39 m
Replace V₁ with 0.25V₂ (from continuity):
20.39 + ((0.25V₂)²)/(19.62) + 0.2 = (V₂²)/(19.62)
Simplify:
20.59 + (0.0625V₂²)/19.62 = (V₂²)/19.62
Multiply through by 19.62:
20.59×19.62 + 0.0625V₂² = V₂²
404 + 0.0625V₂² = V₂²
Rearranging:
V₂² – 0.0625V₂² = 404
0.9375V₂² = 404
V₂² = 404 / 0.9375 ≈ 430.93
V₂ ≈ 20.75 m/s
Then, V₁ = 0.25 × 20.75 ≈ 5.18 m/s
3. Flow Rate (Q)
Q = A₁ × V₁ = 0.007854 m² × 5.18 m/s ≈ 0.0407 m³/s
4. Determining Velocity at 5m Below the Nozzle (Section 3)
Taking datum at Section 3 (5 m below nozzle):
P₂/γ + (V₂²)/(2g) + Z₂ = P₃/γ + (V₃²)/(2g) + Z₃
Here, P₂ = 0 (at nozzle), Z₂ = 0, Z₃ = 5 m, and P₃ = 0
(20.75²)/(2×9.81) + 0 + 5 = (V₃²)/(2×9.81)
Compute velocity head at Section 2: (20.75²)/(19.62) ≈ 21.94 m
Therefore, 21.94 + 5 = (V₃²)/(19.62) → 26.94 = (V₃²)/(19.62)
V₃² = 26.94 × 19.62 ≈ 528.5
V₃ ≈ 23 m/s
5. Jet Diameter 5m Below the Nozzle
Using the flow rate Q remains constant:
Q = A₃ × V₃ → A₃ = Q/V₃ = 0.0407 m³/s ÷ 23 m/s ≈ 0.00177 m²
The area A₃ is related to the jet diameter d₃ by:
A₃ = (π/4) × d₃² → d₃ = √((4A₃)/π)
d₃ = √((4×0.00177)/π) ≈ 0.047 m = 47 mm
Conclusion
By applying Bernoulli’s equation between the 100mm pipe and the 50mm nozzle, along with the continuity equation, the velocity and flow rate were determined. Further application of Bernoulli’s principle for the jet 5m below the nozzle yielded a jet velocity of approximately 23 m/s, leading to a calculated jet diameter of about 47 mm.