Intersection of Two Jets Analysis
Problem Statement
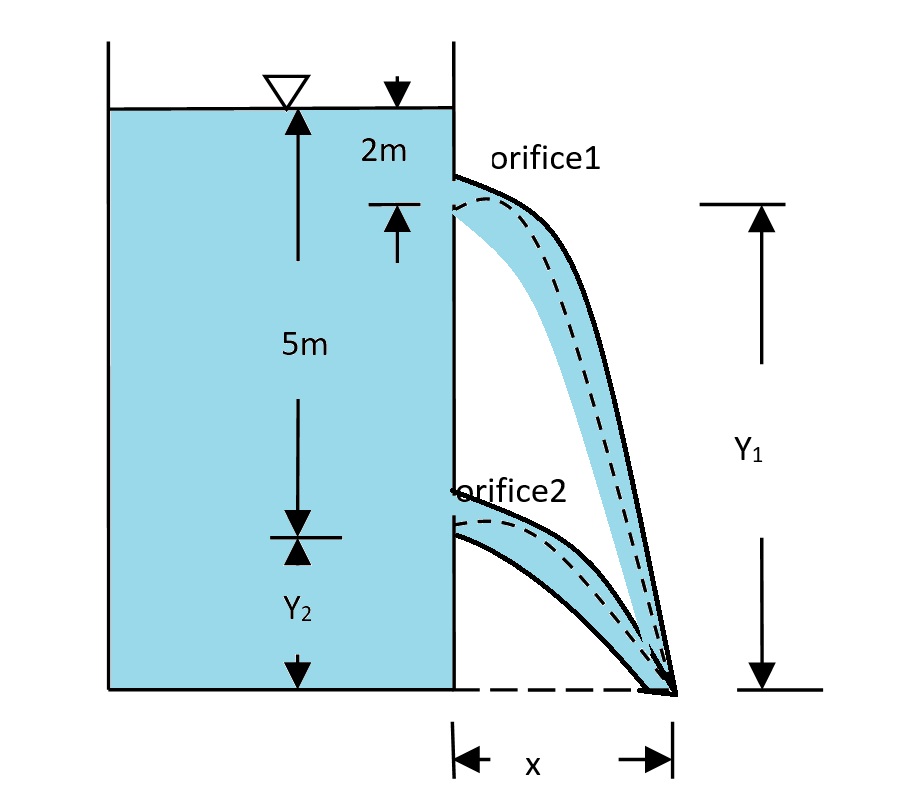
A vessel has two identical orifices provided in one of its sides as shown in the figure. Locate the point of intersection of the two jets. Take Cv = 0.98 for both orifices.
Given Data
| Coefficient of velocity (Cv) | 0.98 |
| Relationship between orifice heights | Y1 = 2.5 Y2 |
| Difference in heights (Y1 – Y2) | 3 m |
1. Establishing the Range Formula
For each orifice, the horizontal range (x) of the jet is given by:
Since both jets have the same Cv and intersect at the same horizontal distance, we equate:
Which simplifies to:
2. Relating the Heights
Given the relationship:
And the difference in heights:
Substituting the first into the second:
3. Calculating the Intersection Point
Using the range formula for one jet:
Assuming the head H1 is 2 m (associated with Y1 = 5 m), we have:
Conclusion
The point of intersection of the two jets is located approximately 6.2 m from the orifice along the horizontal direction.
By using the relationship between the orifice heights (Y1 = 2.5 Y2) and the given height difference (3 m), we determined Y1 = 5 m and Y2 = 2 m. This allowed us to calculate the horizontal range using the formula x = Cv × √(4Y H).