A 500mm pipe carrying 0.8 m3/s of oil (sp gr 0.85) has a 900 bend in a horizontal plane. The loss of head in the bend is 1.1m of oil, and the pressure at the entrance is 290KPa. Determine the resultant force exerted by the oil on the bend.

Pipe Bend Force Calculation

Fluid Mechanics Problem Solution

Problem Statement

A 500mm pipe carrying 0.8 m³/s of oil (sp gr 0.85) has a 90° bend in a horizontal plane. The loss of head in the bend is 1.1m of oil, and the pressure at the entrance is 290kPa. Determine the resultant force exerted by the oil on the bend.

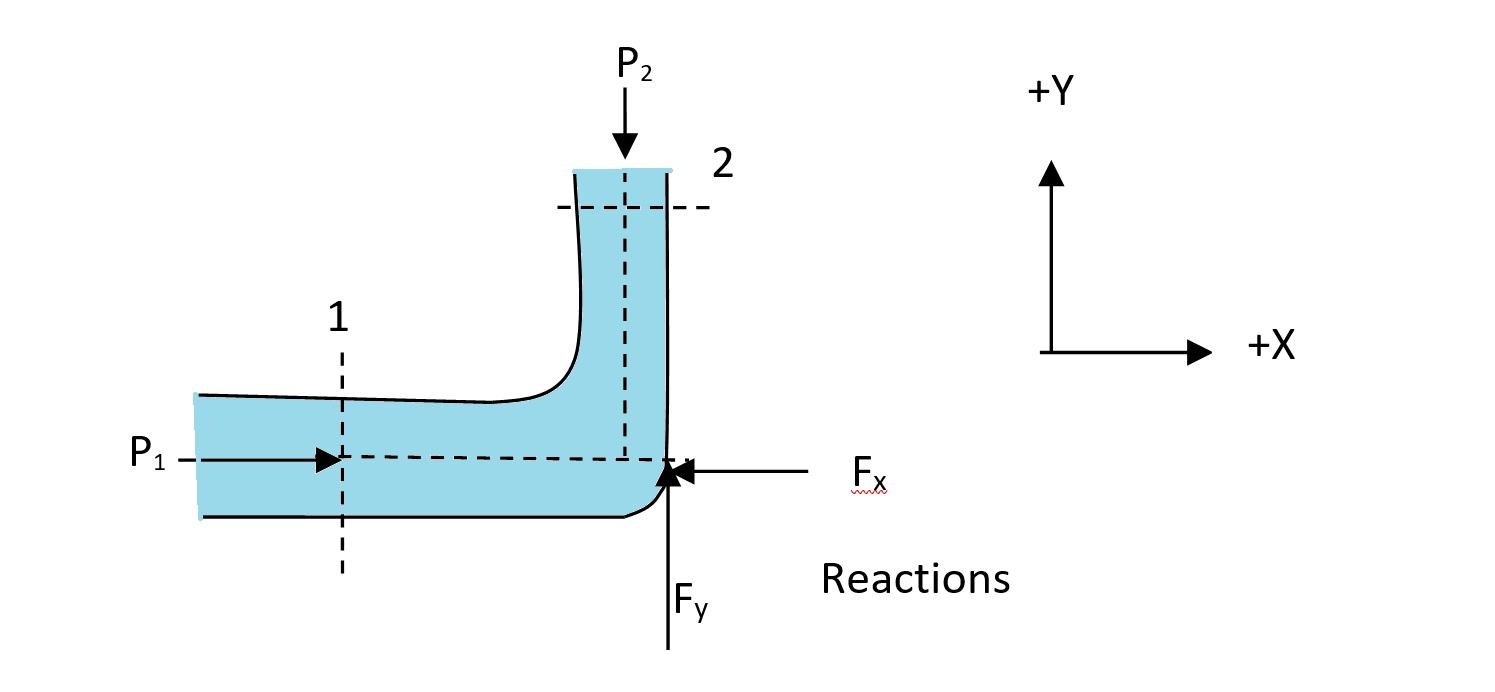
Given Data

Pipe diameter (d)500 mm = 0.5 mFlow rate (Q)0.8 m³/sFluidOil (specific gravity = 0.85)Pressure at entrance (P₁)290 kPa = 290,000 PaHead loss in bend (h_L)1.1 m of oilBend angle90° (in horizontal plane)Fluid density (ρ)0.85 × 1000 = 850 kg/m³

Solution Approach

To find the resultant force exerted by the oil on the bend, we need to:

Calculate the cross-sectional area and velocity in the pipe
Apply Bernoulli's equation to find the pressure at the exit (section 2)
Determine the forces in both X and Y directions using the momentum equation
Calculate the resultant force and its direction

Preliminary Calculations

Step 1: Calculate the cross-sectional area:

A = π/4 × d² = π/4 × 0.5² = 0.19635 m²

Step 2: Calculate the velocity (uniform throughout the pipe):

V = Q/A = 0.8/0.19635 = 4.07 m/s

Applying Bernoulli's Equation

Step 1: Apply Bernoulli's equation between sections 1 and 2 (in a horizontal plane, Z₁ = Z₂):

P₁/ρg + V₁²/2g + Z₁ = P₂/ρg + V₂²/2g + Z₂ + h_L

Step 2: Substitute the values:

290,000/(850×9.81) + 4.07²/(2×9.81) = P₂/(850×9.81) + 4.07²/(2×9.81) + 1.1 34.73 + 0.84 = P₂/(850×9.81) + 0.84 + 1.1 P₂/(850×9.81) = 34.73 - 1.1 = 33.63 P₂ = 33.63 × 850 × 9.81 = 280,828 Pa

Force in X-Direction

Step 1: Apply the momentum equation in the X-direction:

∑Forces in X direction = Rate of change of momentum in X direction P₁A₁ - F_x = ρQ(V₂_x - V₁_x)

Step 2: At section 1, the velocity is entirely in the X-direction (V₁_x = V₁ = 4.07 m/s). At section 2, after the 90° bend, there is no X-component of velocity (V₂_x = 0).

P₁A₁ - F_x = ρQ(0 - 4.07) P₁A₁ - F_x = -ρQV₁

Step 3: Solve for F_x:

F_x = P₁A₁ + ρQV₁ F_x = 290,000 × 0.19635 + 850 × 0.8 × 4.07 F_x = 56,942 + 2,767 = 59,709 N

Force in Y-Direction

Step 1: Apply the momentum equation in the Y-direction:

∑Forces in Y direction = Rate of change of momentum in Y direction F_y - P₂A₂ = ρQ(V₂_y - V₁_y)

Step 2: At section 1, there is no Y-component of velocity (V₁_y = 0). At section 2, after the 90° bend, the velocity is entirely in the Y-direction (V₂_y = V₂ = 4.07 m/s).

F_y - P₂A₂ = ρQ(4.07 - 0) F_y - P₂A₂ = ρQV₂

Step 3: Solve for F_y:

F_y = P₂A₂ + ρQV₂ F_y = 280,828 × 0.19635 + 850 × 0.8 × 4.07 F_y = 55,141 + 2,767 = 57,908 N

Resultant Force Calculation

Step 1: Calculate the magnitude of the resultant force:

F_R = √(F_x² + F_y²) F_R = √(59,709² + 57,908²) F_R = √(3,565,165,681 + 3,353,336,464) F_R = √6,918,502,145 = 83,177 N

Step 2: Calculate the direction of the resultant force:

θ = tan⁻¹(F_y/F_x) = tan⁻¹(57,908/59,709) = 44.10°

The resultant force exerted by the oil on the bend is 83,177 N at an angle of 44.10° (to the right and downward).

Summary

The fluid velocity in the pipe was calculated to be 4.07 m/s.
Using Bernoulli's equation with head loss, we determined the pressure at the exit:
- P₁ = 290,000 Pa (given)
- P₂ = 280,828 Pa (calculated, accounting for the head loss of 1.1 m)
The force components were calculated using the momentum equation:
- X-direction force: F_x = 59,709 N
- Y-direction force: F_y = 57,908 N
The resultant force on the bend:
- Magnitude: 83,177 N
- Direction: 44.10° from the X-axis (to the right and downward)

This problem demonstrates the application of Bernoulli's principle with head loss and the momentum equation in fluid mechanics to determine forces on pipe bends. The resultant force is substantial due to both the pressure forces and the momentum change of the fluid as it changes direction through the 90° bend.