Problem Statement
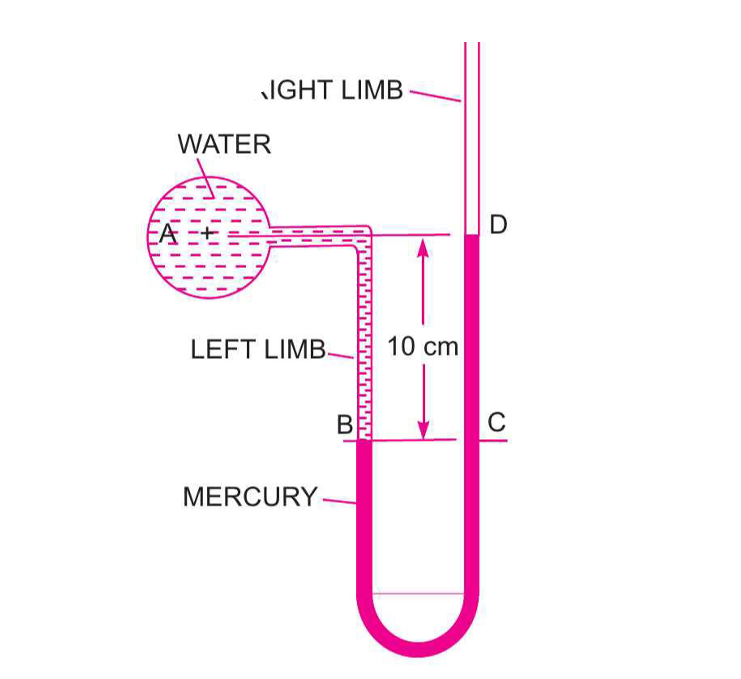
A U-Tube manometer is used to measure the pressure of water in a pipe line, which is in excess of atmospheric pressure. The right limb of the manometer contains mercury and is open to atmosphere. The contact between water and mercury is in the left limb. Determine the pressure of water in the main line, if the difference in level of mercury in the limbs of U-tube is 10 cm and the free surface of mercury is in level with the centre of the pipe. If the pressure of water in pipe line is reduced to 9810 N/m², calculate the new difference in the level of mercury. Sketch the arrangements in both cases.
Given Data
- Fluid in pipe: Water (\(\rho_1 = 1000 \, \text{kg/m}^3\))
- Manometer fluid: Mercury (\(\rho_2 = 13.6 \times 1000 = 13600 \, \text{kg/m}^3\))
- Initial difference in mercury level: \(10 \, \text{cm}\)
- Reduced pressure in pipe (Part 2): \(P'_{A} = 9810 \, \text{N/m}^2\)
Diagrams
Part 1: Initial State
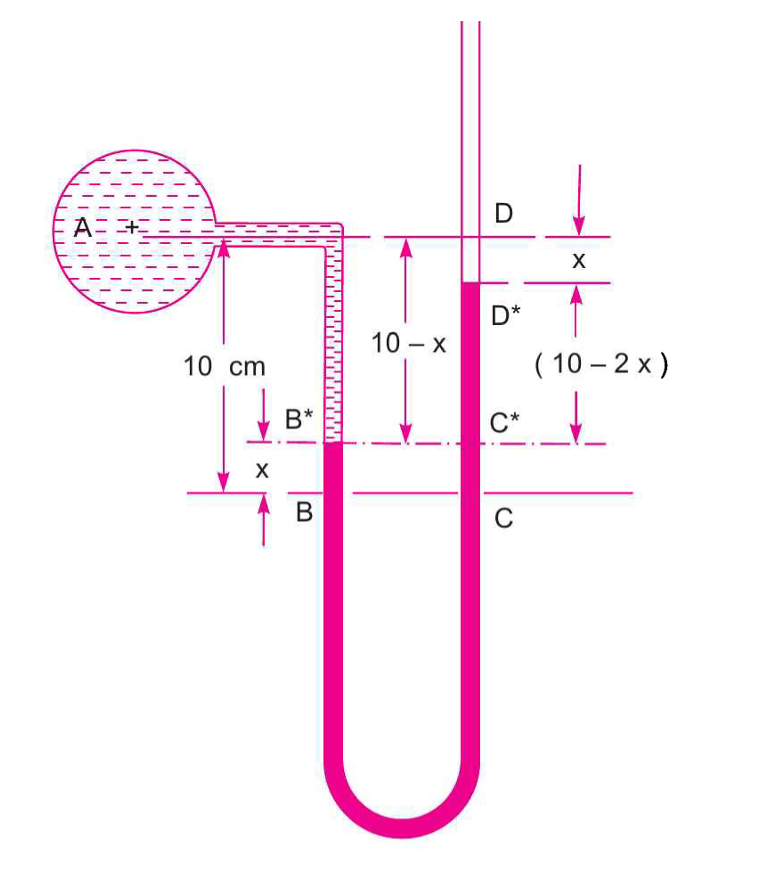
Part 2: Final State
Solution
Part 1: Find Initial Pipe Pressure (\(P_A\))
We establish a datum line at the interface of water and mercury (point B). The pressure at this level is the same in both limbs.
From the diagram, the height of the water column \(h_1\) is 10 cm, and the height of the mercury column \(h_2\) is also 10 cm. The pressure at D is atmospheric (0 gauge pressure).
Now, substitute the values to find \(P_A\).
Part 2: Find New Mercury Level Difference
The pipe pressure is reduced to \(P'_{A} = 9810 \, \text{N/m}^2\). This lower pressure will cause the mercury in the left limb to rise by a distance 'x' and the mercury in the right limb to fall by 'x'.
The new height of the water column is \(h'_{1} = (10 - x)\) cm. The new difference in mercury levels is \(h'_{2} = (10 - 2x)\) cm.
We apply the same manometric equation with the new values.
To simplify, we can divide the entire equation by 9.81.
The new difference in mercury level is \(10 - 2x\).
Part 1: The initial pressure in the pipe is \( \approx 12360.6 \, \text{N/m}^2 \).
Part 2: The new difference in the level of mercury is \( \approx 8.02 \, \text{cm} \).
Explanation of Manometry Principles
This problem uses the fundamental principle of manometry: the pressure at any two points at the same horizontal level within a continuous fluid at rest is equal. By setting a datum line at a convenient point (usually the lower fluid interface), we can write an equation to balance the pressures in the left and right limbs.
The total pressure at the datum in each limb is the sum of the pressure at the top of the limb plus the hydrostatic pressure (\(p = \rho g h\)) of any fluid columns above the datum. When the pressure in the pipe changes, the fluid levels adjust to find a new equilibrium, but the total volume of the manometer fluid (mercury) remains constant. This means a rise of 'x' in one limb must be accompanied by a fall of 'x' in the other.
Physical Meaning
The results show a direct relationship between the pressure in the pipe and the displacement of the mercury. In the first part, the pipe pressure of \(12360.6 \, \text{N/m}^2\) is sufficient to create a 10 cm difference in the mercury levels.
In the second part, when the pipe pressure is reduced to \(9810 \, \text{N/m}^2\), there is less force pushing down on the left side. Consequently, the heavy mercury pushes back, rising in the left limb and falling in the right, until a new equilibrium is reached. The smaller pressure results in a smaller difference in the mercury levels (8.02 cm), which is what we would intuitively expect.