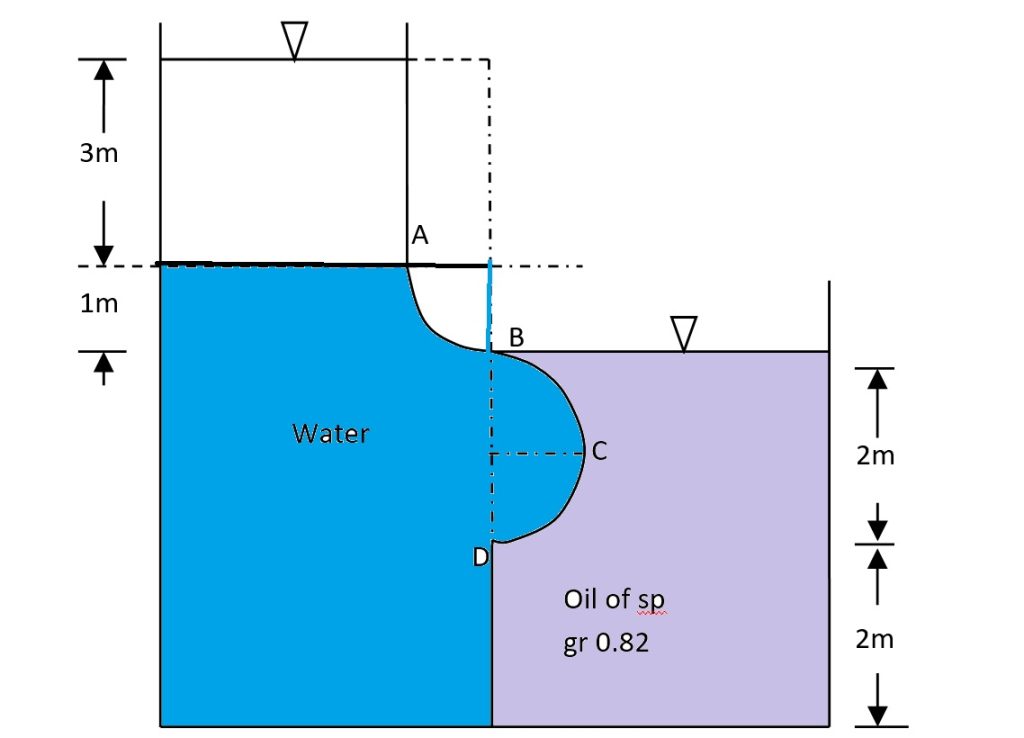
Calculate the pressure force on the curved surface ABCD as shown in the figure below. AB is a quadrant of radius 1m and BCD is a semi-circle of radius 1m. Take width of curve = 5m.
Problem Statement
Calculate the pressure force on the curved surface ABCD as shown in the figure. Given:
- AB is a quadrant of radius 1m
- BCD is a semi-circle of radius 1m
- Width of curve = 5m
- Oil specific gravity = 0.82
- Water above curve section AB
- Water and oil on either side of curve section BCD
Solution
1. Forces on Quadrant AB
Horizontal force on AB:
\( F_{H,AB} = \gamma h A = 9810 \times (1 \times 5) \times 3.5 = 171,675 \, \text{N (right)} \)
Vertical force on AB:
\( F_{V,AB} = 185,674 \, \text{N (up)} \)
2. Forces on Semi-circle BCD (Water Side)
Horizontal force from water:
\( F_{H,BCD,water} = \gamma h A = 9810 \times (2 \times 5) \times 5 = 490,500 \, \text{N (right)} \)
Vertical force from water:
\( F_{V,BCD,water} = 77,048 \, \text{N (down)} \)
3. Forces on Semi-circle BCD (Oil Side)
Horizontal force from oil:
\( F_{H,BCD,oil} = 0.82 \times 9810 \times (2 \times 5) \times 1 = 80,442 \, \text{N (left)} \)
Vertical force from oil:
\( F_{V,BCD,oil} = 63,179 \, \text{N (up)} \)
4. Net Forces
Net horizontal force:
\( F_{H,net} = 171,675 + 490,500 – 80,442 = 581,733 \, \text{N} = 581.733 \, \text{kN (right)} \)
Net vertical force:
\( F_{V,net} = 185,674 – 77,048 + 63,179 = 171,805 \, \text{N} = 171.805 \, \text{kN (up)} \)
Final Results:
- Net Horizontal Force = 581.733 kN (right)
- Net Vertical Force = 171.805 kN (up)
Explanation
- Forces on AB: The quadrant experiences both horizontal and vertical components due to water pressure. The force increases with depth.
- Forces on BCD: The semi-circle experiences opposing forces from water and oil. The water pressure is greater due to higher specific gravity and depth.
- Net Forces: The resultant forces are the sum of all components, considering their directions. The right-directed and upward forces are considered positive.
Physical Meaning
This problem demonstrates several important fluid mechanics principles:
- Pressure Distribution: Hydrostatic pressure increases linearly with depth, affecting both the magnitude and distribution of forces.
- Multiple Fluid Interfaces: The presence of two fluids with different specific gravities creates opposing forces on the curved surface.
- Surface Geometry: The curved surface geometry (quadrant and semi-circle) affects how the pressure forces are resolved into horizontal and vertical components.
- Applications: These calculations are crucial for designing:
- Dam gates and spillways
- Storage tanks with curved surfaces
- Submarine structures
- Pipeline systems
