Determine the total pressure on a circular plate of diameter 1.5 m which is placed vertically in water in such a way that the center of the plate is 3 m below the free surface of water. Find the position of the center of pressure also.

Fluid Pressure on a Vertical Circular Plate

Problem Statement

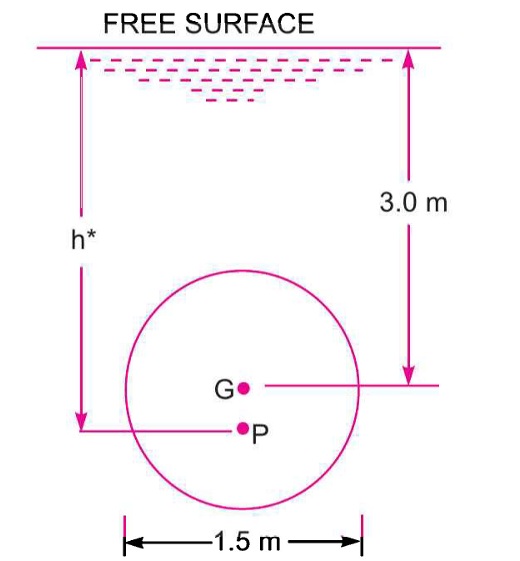
Determine the total pressure on a circular plate of diameter 1.5 m which is placed vertically in water in such a way that the centre of the plate is 3 m below the free surface of water. Find the position of the centre of pressure also.

Given Data

Diameter of plate, $d = 1.5 \, \text{m}$
Area of plate, $A = \frac{\pi}{4}d^2 = \frac{\pi}{4}(1.5)^2 = 1.767 \, \text{m}^2$
Depth of centre of plate, $\bar{h} = 3.0 \, \text{m}$
Density of water, $\rho = 1000 \, \text{kg/m}^3$
Acceleration due to gravity, $g = 9.81 \, \text{m/s}^2$

Diagram

Visual representation of the submerged circular plate.

Solution

(i) Total Pressure (Hydrostatic Force)

The total pressure (force) on the plate is given by the formula:

$$ F = \rho g A \bar{h} $$

Substitute the given values:

$$ F = 1000 \times 9.81 \times 1.767 \times 3.0 $$ $$ F = 52002.81 \, \text{N} $$

(ii) Position of Centre of Pressure

The position of the centre of pressure ($h^*$) is given by the formula:

$$ h^* = \frac{I_G}{A\bar{h}} + \bar{h} $$

Where $I_G$ is the moment of inertia of the circular plate about its centroidal axis, given by:

$$ I_G = \frac{\pi d^4}{64} $$

Calculate the moment of inertia:

$$ I_G = \frac{\pi \times (1.5)^4}{64} = 0.2485 \, \text{m}^4 $$

Now, substitute the values into the equation for $h^*$:

$$ h^* = \frac{0.2485}{1.767 \times 3.0} + 3.0 $$ $$ h^* = 0.0468 + 3.0 $$ $$ h^* = 3.0468 \, \text{m} $$

Final Results:

Total Pressure (Force): $ F = 52002.81 \, \text{N} $

Position of Centre of Pressure: $ h^* = 3.0468 \, \text{m} $ below the free surface

Explanation of Concepts

Total Pressure (Hydrostatic Force): This is the net force exerted by the fluid on the submerged surface. Since fluid pressure increases with depth, the pressure is not uniform across the plate. However, the total force can be conveniently calculated by multiplying the area of the surface ($A$) by the pressure at its geometric center, or centroid ($\rho g \bar{h}$).

Centre of Pressure ($h^*$): This is the specific point on the submerged surface where the total hydrostatic force ($F$) can be considered to act. Because the pressure is greater on the lower parts of the plate than on the upper parts, this point is always located deeper than the geometric centre (centroid) of the surface for any non-horizontal plane.

Physical Meaning

The result shows that the centre of pressure ($h^* = 3.0468 \, \text{m}$) is located slightly below the centroid of the plate ($\bar{h} = 3.0 \, \text{m}$). This is a critical concept in engineering design.

The pressure from the water creates a distributed load on the plate, which is stronger at the bottom than at the top. The "centre of pressure" is the effective point of application for this entire load. Knowing this exact location is essential for designing the plate and its supports to withstand the bending moments and stresses caused by the water pressure without failing. Placing a support at the centroid would be incorrect and could lead to structural failure.