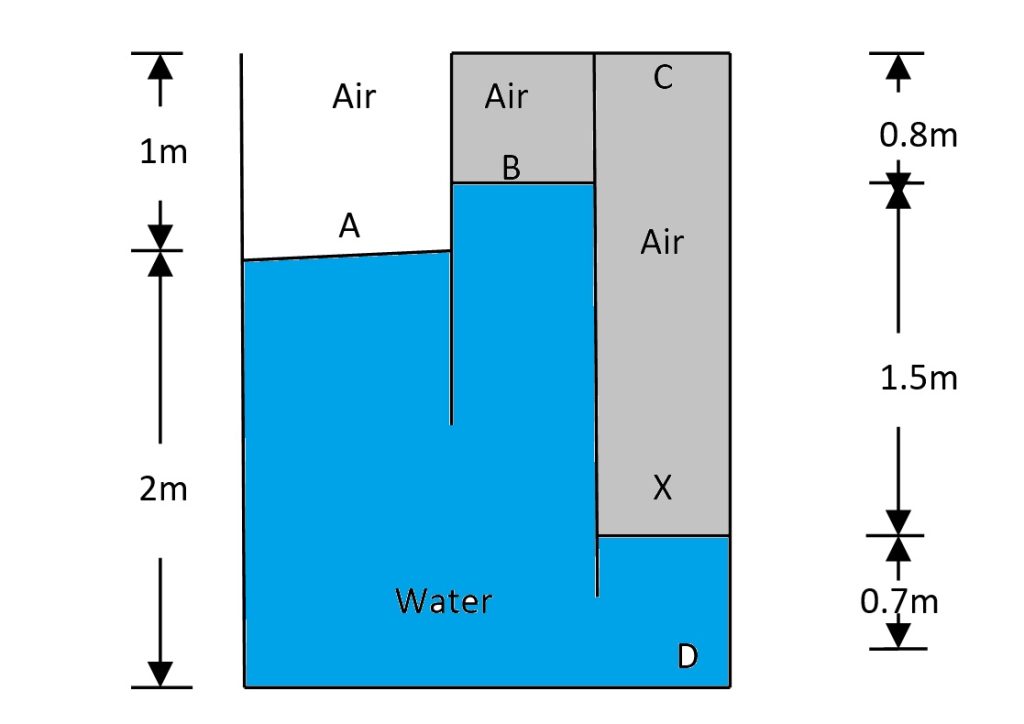
Problem Statement
Given a closed tank, the density of air is \( 1.2 \, \text{kg/m}^3 \), and the density of water is \( 1000 \, \text{kg/m}^3 \). The absolute pressure at point A is \( 2900 \, \text{N/m}^2 \). Determine the absolute pressures at points B, C, and D. Assume the following distances:
- Distance between A and B: \( 0.2 \, \text{m} \)
- Distance between A and X: \( 1.3 \, \text{m} \)
- Distance between X and C: \( 2.3 \, \text{m} \)
- Distance between A and D: \( 2.0 \, \text{m} \)
Solution
Given:
- \( \rho = 1000 \, \text{kg/m}^3 \) (density of water)
- \( \rho_{\text{air}} = 1.2 \, \text{kg/m}^3 \)
- \( P_A = 2900 \, \text{N/m}^2 \)
Pressure at Point B (\( P_B \)):
Using the hydrostatic pressure equation:
\( P_B = P_A – \rho g h_{\text{between A and B}} \)
Substitute the values:
\( P_B = 2900 – (1000 \times 9.81 \times 0.2) \)
Final Value:
\( P_B = 938 \, \text{N/m}^2 \)
Pressure at Point C (\( P_C \)):
Considering the contributions from water and air columns:
\( P_C = P_A + \rho g h_{\text{between A and X}} – \rho_{\text{air}} g h_{\text{XC}} \)
Substitute the values:
\( P_C = 2900 + (1000 \times 9.81 \times 1.3) – (1.2 \times 9.81 \times 2.3) \)
Final Value:
\( P_C = 15626 \, \text{N/m}^2 \)
Pressure at Point D (\( P_D \)):
Using the hydrostatic pressure equation:
\( P_D = P_A + \rho g h_{\text{between A and D}} \)
Substitute the values:
\( P_D = 2900 + (1000 \times 9.81 \times 2) \)
Final Value:
\( P_D = 22520 \, \text{N/m}^2 \)
Explanation
This problem uses the principles of hydrostatics to determine the pressures at different points:
- The pressure at any point in a fluid depends on the density of the fluid, gravitational acceleration, and height difference.
- In this case, the pressure contributions are calculated using water’s density for liquid columns and air’s density for gaseous columns.
- The small density of air (\( \rho_{\text{air}} \)) compared to water results in a minor pressure contribution from the air column.
Physical Meaning
- Density (\( \rho \)): The density of a fluid directly influences its pressure contribution. Water, being denser, has a much greater impact than air.
- Hydrostatic Pressure: The difference in pressure between points arises due to height differences and fluid density. This principle applies in both liquid and gas columns.
- Negligible Air Pressure: While air’s pressure contribution is small, it is included here for completeness, demonstrating how its effect becomes insignificant in most practical scenarios.

