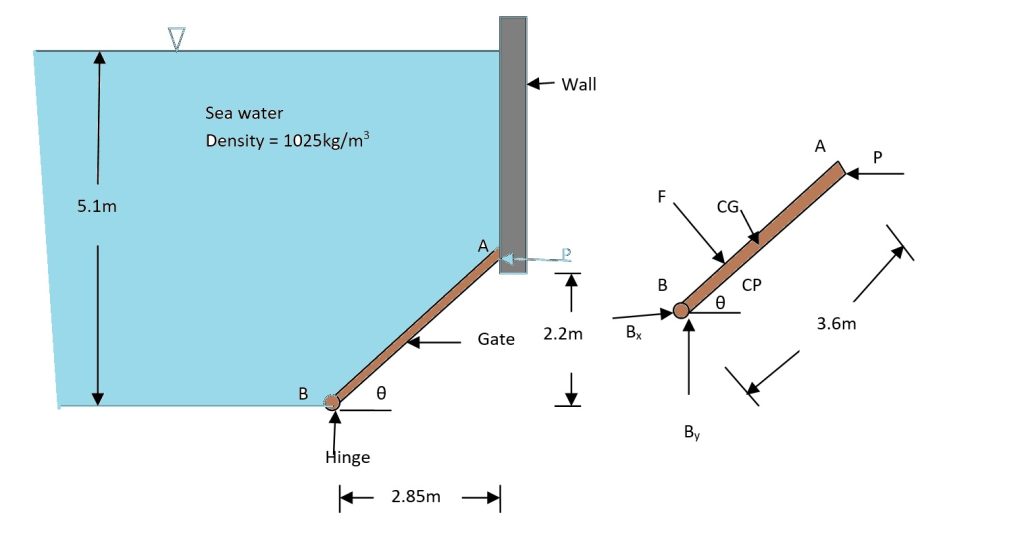
Problem Statement
The gate in the figure is 1.2 m wide, hinged at point B, and rests against a smooth wall at A. Compute:
- (a) The force on the gate due to sea water pressure
- (b) The horizontal force exerted by the wall at point A
- (c) The reaction at hinge B
Solution
1. Specific Weight of Sea Water
The specific weight of sea water is:
\( \gamma = 1025 \times 9.81 = 10055 \, \text{N/m}^3 \)
2. Area of the Gate
The area of the gate is:
\( A = 1.2 \times 3.6 = 4.32 \, \text{m}^2 \)
3. Location of Center of Gravity (CG)
The depth of the CG from the free surface is:
\( y_{\text{CG}} = (5.1 – 2.2) + \frac{2.2}{2} = 4.0 \, \text{m} \)
4. Resultant Force on the Gate
The resultant force is:
\( F = \gamma \cdot A \cdot y_{\text{CG}} \)
\( F = 10055 \times 4.32 \times 4.0 = 173750 \, \text{N} = 173.75 \, \text{kN} \)
5. Horizontal Force at Point A
The moment of inertia about the CG is:
\( I_G = \frac{1}{12} \times 1.2 \times 3.6^3 = 4.665 \, \text{m}^4 \)
The vertical distance of the center of pressure (CP) from the free surface is:
\( y_p = y_{\text{CG}} + \frac{I_G \cdot \sin^2 \theta}{A \cdot y_{\text{CG}}} \)
\( y_p = 4.0 + \frac{4.665 \times (2.2/3.6)^2}{4.32 \times 4.0} = 4.1 \, \text{m} \)
The distance between CP and B is:
\( \Delta y = 5.1 – 4.1 = 1.0 \, \text{m} \)
Taking moments about B:
\( P \cdot 2.2 – 173.75 \cdot 1.636 = 0 \)
\( P = 129.2 \, \text{kN} \)
6. Reactions at Hinge B
Using horizontal force balance:
\( B_x – 129.2 = 0 \)
\( B_x = 23.02 \, \text{kN} \)
Using vertical force balance:
\( B_y – 173.75 \cdot \frac{2.85}{3.6} = 0 \)
\( B_y = 137.55 \, \text{kN} \)
Results:
- Resultant Force: \( F = 173.75 \, \text{kN} \)
- Horizontal Force at Point A: \( P = 129.2 \, \text{kN} \)
- Reactions at Hinge B: \( B_x = 23.02 \, \text{kN}, \; B_y = 137.55 \, \text{kN} \)
Explanation
- Specific Weight: The specific weight is calculated using the density of sea water and the acceleration due to gravity.
- Center of Gravity: The CG is determined based on the gate’s dimensions and position relative to the hinge.
- Resultant Force: The hydrostatic force is based on the depth of the CG and the area of the gate.
- Horizontal Force: Moments are taken about the hinge to calculate the horizontal force exerted by the wall.
- Reactions at Hinge: Horizontal and vertical force balances are used to find the reactions at hinge B.
Physical Meaning
This problem highlights the principles of hydrostatic pressure on submerged gates and their implications for structural stability. Engineers use these calculations to design gates and hinges capable of withstanding fluid forces while maintaining functionality.