Problem Statement
The figure below shows a conical vessel with an outlet at A connected to a U-tube manometer. The initial reading of the manometer is shown when the vessel is empty. Find the reading of the manometer when the vessel is completely filled with water.
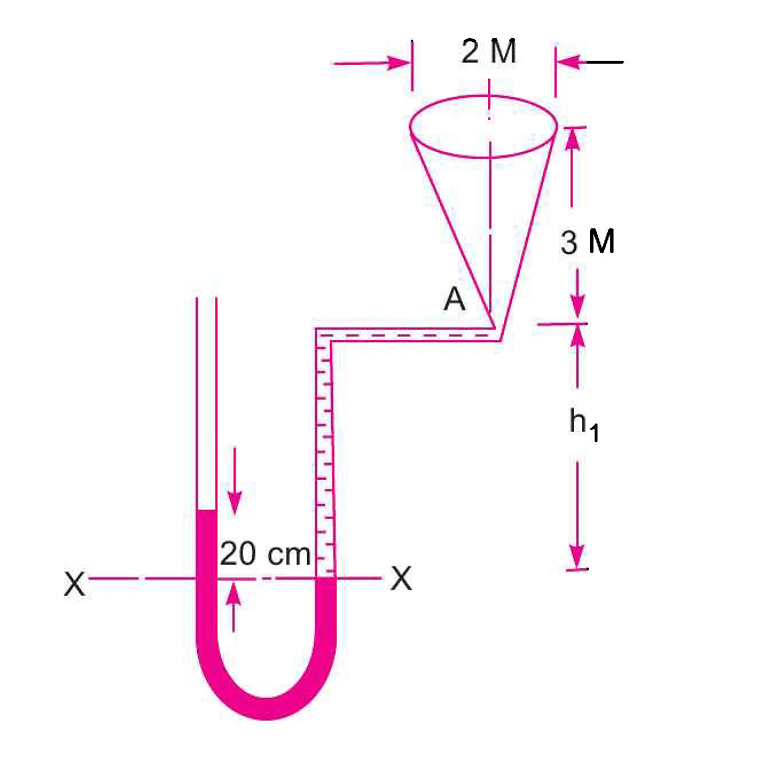
Given Data (Empty Vessel)
- Initial difference in mercury level, \(h_2 = 20 \, \text{cm} = 0.2 \, \text{m}\)
- Height of vessel to be filled = 3 m
- Specific gravity of mercury, \(S_{Hg} = 13.6\)
- Specific gravity of water, \(S_{w} = 1.0\)
Solution
Part 1: Analyze the Empty Vessel
First, we analyze the initial state to find the height of the water column in the left limb, \(h_1\), that is balancing the mercury. The datum line X-X is at the mercury-water interface.
Part 2: Analyze the Full Vessel
When the vessel is filled, the pressure at A increases, pushing the mercury down by a distance \(y\) in the right limb and up by \(y\) in the left limb. The new datum line Z-Z is at the new, lower mercury level in the right limb.
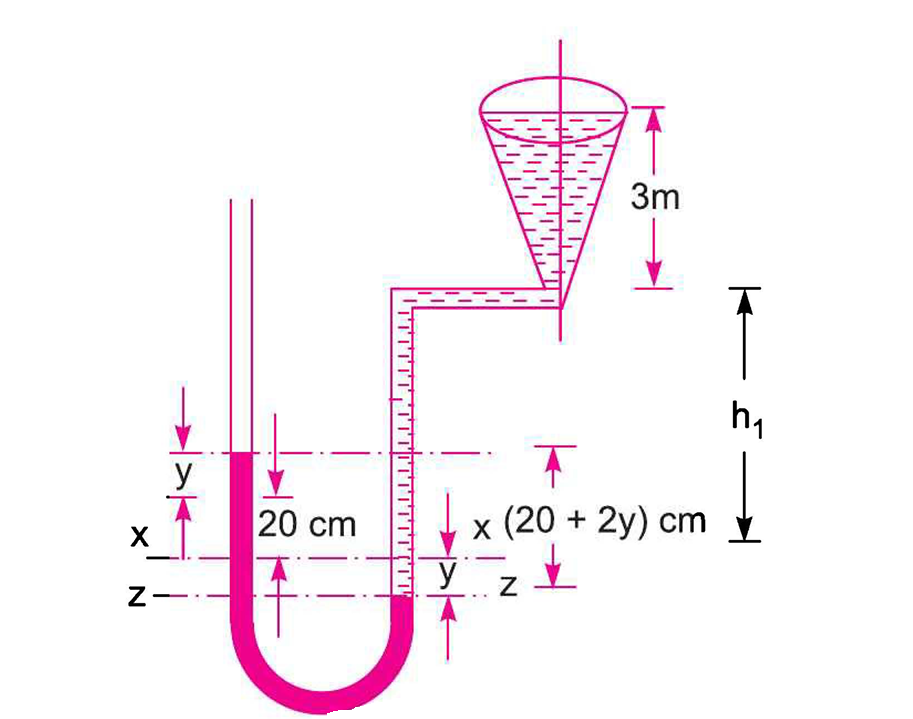
We equate the pressures at the new datum line Z-Z.
We can cancel \(g\) and substitute the known densities and \(h_1\):
3. Find the New Manometer Reading
The new difference in mercury levels is the original difference plus the movement in both limbs (\(2y\)).
The reading of the manometer when the vessel is full is \( 42.9 \, \text{cm} \).
Explanation of the Method
Step 1: Initial State Analysis. The "empty" vessel isn't truly empty; the manometer setup implies a column of water in the left tube is balancing the initial 20 cm of mercury. The first step is crucial to find the height of this initial water column (\(h_1\)). This value is needed for the final calculation.
Step 2: Final State Analysis. When the 3-metre vessel is filled with water, the pressure at point A increases significantly. This new pressure is transmitted to the manometer. We model this by assuming the mercury in the right limb is pushed down by a distance \(y\), which forces the mercury in the left limb to rise by the same distance \(y\). By setting up a new pressure balance equation at a new datum line (the lowest mercury level), we can solve for this unknown displacement \(y\).
Step 3: Final Reading. The new manometer reading is the total vertical distance between the two mercury levels. This is the original 20 cm difference, plus the distance the right side went down (\(y\)), plus the distance the left side went up (\(y\)), giving a total of \(20 + 2y\).
Physical Meaning
The final manometer reading of 42.9 cm represents the gauge pressure at the outlet A when the vessel is full of water. The large increase from the initial 20 cm reading is a direct result of the pressure exerted by the 3-metre column of water added to the system.
This problem demonstrates how manometers can be used to measure pressure changes in a system. The displacement of the heavy mercury provides a magnified and easily measurable indication of the change in pressure caused by filling the vessel. The final state is an equilibrium where the total pressure from the tall column of water is balanced by the pressure from the much shorter but denser column of mercury.